4051. Grasshopper

Grasshopper lives in the teacher's room. It likes to jump on one dimensional checkerboard. The length of the board is n cells. To its regret, it can jump only on 1, 2, ..., k cells forward.

Once teachers wondered in how many ways a grasshopper can reach the last cell from the first one. Help them to answer this question.

Input. Two integers n and k (1 ≤ n ≤ 30, 1 ≤ k ≤ 10).

Output. Print the number of ways for grasshopper to leap from the first cell to the last.

Sample input	Sample output
8 2	21

SOLUTION

dynamic programming

Algorithm analysis

Let dp[i] equals to the number of ways for grasshopper to leap from the first cell to the i-th one. Set dp[1] = 1, dp[2] = 1.

If 2 < i ≤ k, then its possible to get into the i-th cell from any previous one, so

dp[i] = dp[1] + dp[2] + … + dp[i – 1] =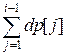

Let k be large, calculate dp[i] using this formula:

dp[3] = dp[1] + dp[2] = 1 + 1 = 2,

dp[4] = dp[1] + dp[2] + dp[3] = 1 + 1 + 2 = 4,

dp[5] = dp[1] + dp[2] + dp[3] + dp[4] = 1 + 1 + 2 + 4 = 8

You can notice that dp[i] = 2* dp[i – 1]. However, this formula can be obtained from the following considerations. From

dp[i – 1] = dp[1] + dp[2] + … + dp[i – 2]

follows that

dp[i] = (dp[1] + dp[2] + … + dp[i – 2]) + dp[i – 1] =

dp[i – 1] + dp[i – 1] = 2 * dp[i – 1]

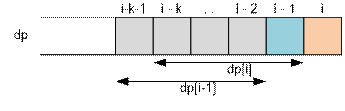
If i > k, then its possible to get into the i-th cell from any out of k previous, so

dp[i] = = dp[i – k] + … + dp[i – 1]

Similarly, you can see that from the fact that

dp[i – 1] = dp[i – k – 1] + … + dp[i – 2]

follows that

dp[i] = dp[i – k] + … + dp[i – 1] =

(dp[i – k – 1] + dp[i – k] + … + dp[i – 2]) – dp[i – k – 1] + dp[i – 1] =

2 * dp[i – 1] – dp[i – k – 1]

Sample

For the given sample test n = 8 and k = 2 the state of dp array has the from:

For n = 8 and k = 4 the array dp has the form:

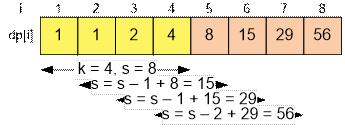
Exercise

Fill dp array for n = 8 and k = 3.

Algorithm realization

Declare the array.

#define MAX 35

int dp[MAX];

Read the input data. Initialize dp[1] = dp[2] = 1.

scanf("%d %d",&n,&k);

dp[1] = 1; dp[2] = 1;

Fill cells of array dp[i] for 2 < i ≤ k.

for(i = 3; i <= k; i++)

dp[i] = 2 * dp[i-1];

Fill cells of array dp[i] for i > k.

for(; i <= n; i++)

dp[i] = 2 * dp[i-1] - dp[i-k-1];

Print the answer.

printf("%d\n",dp[n]);

Java realization

import java.util.*;

class Main

{

static int dp[] = new int[35];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int k = con.nextInt();

int i;

dp[1] = 1; dp[2] = 1;

for(i = 3; i <= k; i++)

dp[i] = 2 * dp[i-1];

for(; i <= n; i++)

dp[i] = 2 * dp[i-1] - dp[i-k-1];

System.out.println(dp[n]);

con.close();

}

}